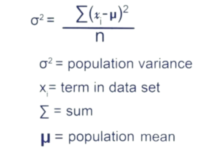Standar Deviasi adalah salah satu konsep yang penting dalam statistik yang digunakan untuk mengukur sejauh mana data tersebar dari nilai rata-rata. Dalam analisis data, rumus Standar Deviasi Manual sangat diperlukan untuk melakukan perhitungan secara manual tanpa menggunakan perangkat lunak statistik. Dalam artikel ini, kami akan memberikan panduan lengkap dan terperinci tentang rumus Standar Deviasi Manual, serta memberikan contoh yang jelas untuk memahaminya dengan lebih baik.
Sebelum kita memahami rumus Standar Deviasi Manual, penting untuk mengetahui konsep dasar tentang mean atau rata-rata. Rata-rata adalah jumlah dari semua nilai dalam suatu dataset, dibagi dengan jumlah total nilai dalam dataset tersebut. Untuk menghitung Standar Deviasi Manual, kita perlu mengurangi setiap nilai dalam dataset dengan rata-rata, kemudian mengkuadratkannya, menjumlahkannya, dan kemudian mengambil akar kuadrat dari hasil tersebut. Rumus ini mungkin terdengar rumit, tetapi dengan panduan yang tepat, kita dapat menggunakannya dengan mudah dan akurat.
Menghitung Rata-rata
Langkah pertama dalam rumus Standar Deviasi Manual adalah menghitung rata-rata dari dataset yang diberikan. Rata-rata adalah jumlah dari semua nilai dalam dataset, dibagi dengan jumlah total nilai dalam dataset tersebut. Untuk menghitung rata-rata, kita perlu menjumlahkan semua nilai dalam dataset dan kemudian membaginya dengan jumlah total nilai. Misalnya, jika kita memiliki dataset yang terdiri dari 5 nilai yaitu 10, 15, 20, 25, dan 30, maka rata-rata dapat dihitung dengan menjumlahkan semua nilai tersebut (10 + 15 + 20 + 25 + 30 = 100) dan kemudian membaginya dengan jumlah total nilai (100 / 5 = 20). Jadi, rata-rata dari dataset ini adalah 20.
Summary: Menghitung rata-rata adalah langkah pertama dalam rumus Standar Deviasi Manual. Ini melibatkan menjumlahkan semua nilai dalam dataset dan membaginya dengan jumlah total nilai.
Contoh Perhitungan Rata-rata
Untuk memberikan contoh yang lebih jelas tentang bagaimana menghitung rata-rata, mari kita gunakan dataset yang terdiri dari 7 nilai yaitu 12, 15, 18, 21, 24, 27, dan 30. Pertama, kita menjumlahkan semua nilai tersebut: 12 + 15 + 18 + 21 + 24 + 27 + 30 = 147. Selanjutnya, kita membagi jumlah total tersebut dengan jumlah nilai dalam dataset, yaitu 7. Jadi, rata-rata dari dataset ini adalah 147 / 7 = 21.
Summary: Dalam contoh ini, kita menggunakan dataset yang terdiri dari 7 nilai untuk menghitung rata-rata. Setelah menjumlahkan semua nilai, kita membaginya dengan jumlah total nilai dalam dataset untuk mendapatkan rata-rata.
Penyimpangan dari Rata-rata
Setelah kita menghitung rata-rata, langkah selanjutnya dalam rumus Standar Deviasi Manual adalah menghitung penyimpangan dari rata-rata. Penyimpangan dari rata-rata adalah selisih antara setiap nilai dalam dataset dengan rata-ratanya. Untuk melakukan ini, kita perlu mengurangi setiap nilai dengan rata-rata. Misalnya, jika rata-rata adalah 20 dan kita memiliki dataset yang terdiri dari nilai 15, 25, dan 30, maka penyimpangan dari rata-rata dapat dihitung dengan mengurangi rata-rata dari setiap nilai dalam dataset: 15 – 20 = -5, 25 – 20 = 5, 30 – 20 = 10. Jadi, penyimpangan dari rata-rata untuk dataset ini adalah -5, 5, dan 10.
Summary: Penyimpangan dari rata-rata adalah selisih antara setiap nilai dalam dataset dengan rata-ratanya. Ini melibatkan mengurangi setiap nilai dengan rata-rata.
Mengkuadratkan Penyimpangan
Setelah kita menghitung penyimpangan dari rata-rata, langkah berikutnya dalam rumus Standar Deviasi Manual adalah mengkuadratkan penyimpangan tersebut. Mengkuadratkan penyimpangan adalah mengalikan setiap penyimpangan dengan dirinya sendiri. Misalnya, jika kita memiliki dataset dengan nilai penyimpangan -5, 5, dan 10, maka kita perlu mengkuadratkan setiap nilai ini: (-5)^2 = 25, 5^2 = 25, dan 10^2 = 100. Jadi, nilai kuadrat dari penyimpangan ini adalah 25, 25, dan 100.
Summary: Mengkuadratkan penyimpangan melibatkan mengalikan setiap penyimpangan dengan dirinya sendiri.
Jumlah Nilai Kuadrat
Setelah mengkuadratkan setiap penyimpangan, langkah selanjutnya dalam rumus Standar Deviasi Manual adalah menjumlahkan semua nilai kuadrat yang dihasilkan. Ini dilakukan dengan menjumlahkan semua nilai kuadrat yang telah dihitung sebelumnya. Misalnya, jika kita memiliki dataset dengan nilai kuadrat penyimpangan 25, 25, dan 100, maka kita perlu menjumlahkan semua nilai ini: 25 + 25 + 100 = 150. Jadi, jumlah nilai kuadrat untuk dataset ini adalah 150.
Summary: Menjumlahkan nilai kuadrat melibatkan menjumlahkan semua nilai kuadrat penyimpangan yang telah dihitung sebelumnya.
Menghitung Varians
Setelah menjumlahkan semua nilai kuadrat, langkah berikutnya dalam rumus Standar Deviasi Manual adalah menghitung varians. Varians adalah rata-rata dari nilai kuadrat yang telah dihasilkan. Untuk menghitung varians, kita perlu membagi jumlah nilai kuadrat dengan jumlah total nilai dalam dataset. Misalnya, jika jumlah nilai kuadrat adalah 150 dan kita memiliki dataset dengan jumlah nilai 5, maka varians dapat dihitung dengan membagi jumlah nilai kuadrat dengan jumlah total nilai: 150 / 5 = 30. Jadi, varians dari dataset ini adalah 30.
Summary: Varians adalah rata-rata dari nilai kuadrat penyimpangan. Untuk menghitung varians, kita membagi jumlah nilai kuadrat dengan jumlah total nilai dalam dataset.
Mengambil Akar Kuadrat
Setelah menghitung varians, langkah terakhir dalam rumus Standar Deviasi Manual adalah mengambil akar kuadrat dari nilai varians. Ini dilakukan untuk mendapatkan nilai Standar Deviasi yang sesuai dengan skala data asli. Untuk mengambil akar kuadrat, kita perlu menggunakan fungsi akar kuadrat pada nilai varians. Misalnya, jika varians adalah 30, maka akar kuadrat dari 30 dapat dihitung menggunakan fungsi akar kuadrat: √30 ≈ 5.48. Jadi, Standar Deviasi dari dataset ini adalah sekitar 5.48.
Summary: Mengambil akar kuadrat dari nilai varians dilakukan untuk mendapatkan nilai Standar Deviasi yang sesuai dengan skala data asli. Ini melibatkan penggunaan fungsi akar kuadrat pada nilai varians.
Contoh Perhitungan Standar Deviasi Manual
Dalam sesi ini, kita akan memberikan contoh perhitungan Standar Deviasi Manual secara keseluruhan. Dengan contoh yang jelas, kita akan memahami bagaimana mengaplikasikan rumus dan langkah-langkah yang telah kita pelajari sebelumnya.
Contoh Dataset
Untuk contoh perhitungan kita, mari kita gunakan dataset yang terdiri dari 8 nilai yaitu 10, 15, 20, 25, 30, 35, 40, dan 45.
Langkah 1: Menghitung Rata-rata
Langkah pertama adalah menghitung rata-rata dari dataset. Untuk dataset ini, kita dapat menjumlahkan semua nilai: 10 + 15 + 20 + 25 + 30 + 35 + 40 + 45 =220. Setelah itu, kita membagi jumlah total tersebut dengan jumlah nilai dalam dataset, yaitu 8. Jadi, rata-rata dari dataset ini adalah 220 / 8 = 27.5.
Langkah 2: Penyimpangan dari Rata-rata
Selanjutnya, kita perlu menghitung penyimpangan dari rata-rata. Untuk setiap nilai dalam dataset, kita mengurangi nilai tersebut dengan rata-rata yang telah dihitung sebelumnya. Misalnya, untuk nilai 10, penyimpangannya adalah 10 – 27.5 = -17.5. Kita melakukan hal yang sama untuk setiap nilai dalam dataset dan mendapatkan penyimpangan sebagai berikut:
- 10 – 27.5 = -17.5
- 15 – 27.5 = -12.5
- 20 – 27.5 = -7.5
- 25 – 27.5 = -2.5
- 30 – 27.5 = 2.5
- 35 – 27.5 = 7.5
- 40 – 27.5 = 12.5
- 45 – 27.5 = 17.5
Summary: Penyimpangan dari rata-rata adalah selisih antara setiap nilai dalam dataset dengan rata-ratanya. Kita mengurangi setiap nilai dengan rata-rata yang telah dihitung sebelumnya.
Langkah 3: Mengkuadratkan Penyimpangan
Sekarang, kita perlu mengkuadratkan penyimpangan yang telah dihitung sebelumnya. Untuk setiap nilai penyimpangan, kita mengalikan nilai tersebut dengan dirinya sendiri. Misalnya, untuk penyimpangan -17.5, kita mengkuadratkannya menjadi (-17.5)^2 = 306.25. Kita melakukan hal yang sama untuk setiap nilai penyimpangan dan mendapatkan hasil kuadrat sebagai berikut:
- (-17.5)^2 = 306.25
- (-12.5)^2 = 156.25
- (-7.5)^2 = 56.25
- (-2.5)^2 = 6.25
- (2.5)^2 = 6.25
- (7.5)^2 = 56.25
- (12.5)^2 = 156.25
- (17.5)^2 = 306.25
Summary: Mengkuadratkan penyimpangan melibatkan mengalikan setiap penyimpangan dengan dirinya sendiri.
Langkah 4: Jumlah Nilai Kuadrat
Selanjutnya, kita perlu menjumlahkan semua nilai kuadrat yang telah dihasilkan. Kita menjumlahkan semua nilai kuadrat tersebut: 306.25 + 156.25 + 56.25 + 6.25 + 6.25 + 56.25 + 156.25 + 306.25 = 1050. Jadi, jumlah nilai kuadrat untuk dataset ini adalah 1050.
Summary: Menjumlahkan nilai kuadrat melibatkan menjumlahkan semua nilai kuadrat penyimpangan yang telah dihitung sebelumnya.
Langkah 5: Menghitung Varians
Selanjutnya, kita perlu menghitung varians dari dataset. Varians adalah rata-rata dari nilai kuadrat penyimpangan. Untuk menghitung varians, kita membagi jumlah nilai kuadrat dengan jumlah total nilai dalam dataset. Dalam kasus ini, jumlah nilai kuadrat adalah 1050 dan jumlah nilai dalam dataset adalah 8. Jadi, varians dapat dihitung dengan membagi 1050 dengan 8: 1050 / 8 = 131.25. Jadi, varians dari dataset ini adalah 131.25.
Summary: Varians adalah rata-rata dari nilai kuadrat penyimpangan. Kita membagi jumlah nilai kuadrat dengan jumlah total nilai dalam dataset untuk menghitung varians.
Langkah 6: Mengambil Akar Kuadrat
Langkah terakhir dalam rumus Standar Deviasi Manual adalah mengambil akar kuadrat dari nilai varians. Ini dilakukan untuk mendapatkan nilai Standar Deviasi yang sesuai dengan skala data asli. Untuk mengambil akar kuadrat, kita perlu menggunakan fungsi akar kuadrat pada nilai varians. Dalam kasus ini, nilai varians adalah 131.25. Jadi, akar kuadrat dari 131.25 dapat dihitung menggunakan fungsi akar kuadrat: √131.25 ≈ 11.47. Jadi, Standar Deviasi dari dataset ini adalah sekitar 11.47.
Summary: Mengambil akar kuadrat dari nilai varians dilakukan untuk mendapatkan nilai Standar Deviasi yang sesuai dengan skala data asli. Ini melibatkan penggunaan fungsi akar kuadrat pada nilai varians.
Keuntungan Menggunakan Rumus Standar Deviasi Manual
Dalam sesi ini, kita akan membahas keuntungan penggunaan rumus Standar Deviasi Manual. Meskipun ada perangkat lunak dan aplikasi yang dapat menghitung Standar Deviasi secara otomatis, memahami dan mampu menghitung secara manual memberikan keunggulan tersendiri.
1. Memahami Konsep Secara Mendalam
Dengan menghitung Standar Deviasi secara manual, kita akan memahami konsep yang mendasarinya dengan lebih mendalam. Kita akan memahami bagaimana setiap langkah dalam rumus berkontribusi terhadap perhitungan akhir. Ini akan membantu kita dalam memahami distribusi data dan sejauh mana data tersebar dari nilai rata-rata.
2. Kontrol Penuh atas Perhitungan
Dengan melakukan perhitungan secara manual, kita memiliki kontrol penuh atas setiap langkah perhitungan. Kita dapat memeriksa setiap langkah untuk memastikan kebenaran dan keakuratan perhitungan. Ini memungkinkan kita untuk mengidentifikasi dan memperbaiki kesalahan jika ditemukan.
3. Fleksibilitas dalam Menggunakan Rumus
Dengan memahami rumus Standar Deviasi Manual, kita dapat dengan mudah mengadaptasinya sesuai dengan kebutuhan dan situasi yang spesifik. Kita dapat memodifikasi rumus untuk memasukkan faktor-faktor tambahan atau mengubah langkah-langkah perhitungan sesuai dengan persyaratan yang diperlukan.
4. Pengembangan Keterampilan Analisis Data
Dengan menghitung Standar Deviasi secara manual, kita akan mengembangkan keterampilan analisis data yang lebih baik. Kita akan menjadi lebih terampil dalam memahami pola data, mengidentifikasi anomali, dan menginterpretasikan hasil perhitungan Standar Deviasi secara lebih efektif.
5. Memahami Keterbatasan dan Batasan Rumus
Dengan menggunakan rumus Standar Deviasi Manual, kita akan memahami keterbatasan dan batasan dari rumus ini. Kita akan dapat mengidentifikasi situasi di mana rumus ini mungkin tidak memberikan hasil yang akurat atau relevan. Ini membantu kita dalam mengambil keputusan yang lebih bijaksana dalam analisis data.
Batasan dan Pertimbangan dalam Rumus Standar Deviasi Manual
Dalam sesi ini, kita akan membahas batasan dan pertimbangan dalam penggunaan rumus Standar Deviasi Manual. Meskipun rumus ini dapat memberikan hasil yang akurat, ada beberapa faktor yang perlu diperhatikan agar perhitungan lebih valid.
1. Ukuran Sampel
Ukuran sampel, yaitu jumlah nilai dalam dataset, dapat mempengaruhi hasil perhitungan Standar Deviasi. Semakin besar ukuran sampel, semakin akurat Standar Deviasi yang dihasilkan. Oleh karena itu, penting untuk memperhatikan ukuran sampel saat menggunakan rumus Standar Deviasi Manual.
2. Keberadaan Pencilan atau Outlier
Kehadiran pencilan atau outlier dalam dataset dapat mempengaruhi perhitungan StandarDeviasi. Outlier adalah nilai yang jauh berbeda dari nilai-nilai lain dalam dataset. Jika dataset mengandung outlier, perhitungan Standar Deviasi dapat menjadi tidak representatif. Oleh karena itu, penting untuk memeriksa keberadaan outlier dan mempertimbangkan untuk menghapusnya atau menggunakan metode lain untuk mengatasi outlier dalam analisis data.
3. Distribusi Data
Rumus Standar Deviasi Manual diasumsikan bahwa data dalam dataset mengikuti distribusi normal atau mendekati distribusi normal. Jika data memiliki distribusi yang tidak simetris atau tidak normal, perhitungan Standar Deviasi mungkin tidak memberikan hasil yang akurat atau relevan. Dalam kasus seperti itu, perlu dipertimbangkan untuk menggunakan metode statistik yang lebih sesuai dengan distribusi data yang ada.
4. Interpretasi Hasil
Pada akhirnya, Standar Deviasi hanyalah salah satu metrik dalam analisis data. Penting untuk menginterpretasikan hasil perhitungan Standar Deviasi dengan hati-hati dan dalam konteks yang tepat. Standar Deviasi mengukur sejauh mana data tersebar dari nilai rata-rata, tetapi tidak memberikan informasi tentang bentuk distribusi atau kecenderungan data. Oleh karena itu, perlu dipertimbangkan untuk menggunakan metrik lain dan menganalisis data secara komprehensif untuk mendapatkan pemahaman yang lebih lengkap tentang dataset.
Kesimpulan
Dalam artikel ini, kita telah membahas rumus Standar Deviasi Manual secara lengkap dan terperinci. Dengan memahami langkah-langkah dalam rumus ini, kita dapat dengan mudah menghitung Standar Deviasi secara manual tanpa menggunakan perangkat lunak statistik. Rumus Standar Deviasi Manual penting dalam analisis data, dan dengan contoh yang jelas, kita dapat mengaplikasikannya dalam praktiknya. Meskipun ada perangkat lunak yang dapat menghitung secara otomatis, memahami rumus secara manual memberikan keunggulan tersendiri dalam pemahaman statistik.
Dengan menggunakan rumus Standar Deviasi Manual, kita dapat memahami distribusi data, mengidentifikasi anomali, dan membuat keputusan yang lebih baik berdasarkan pemahaman yang lebih mendalam tentang variabilitas data. Namun, penting untuk memperhatikan batasan dan pertimbangan dalam penggunaan rumus ini agar perhitungan lebih valid dan interpretasi hasil lebih akurat. Dengan demikian, kita dapat menggunakan rumus Standar Deviasi Manual secara efektif dalam analisis data kita.